OPERACIONES ELEMENTALES DE FOTOGRAMETRÍA ANALÍTICA

3.3. MOVIMIENTOS EN EL ESPACIO

3.3.1 Matriz genérica

Sean los sistemas cartesianos (X Y Z) (X’ Y’ Z’) entre los que media una rotación de tal manera que puede escribirse:

X’		R11 R12 R13		X		X’				X
Y’	=	R21 R22 R23	*	Y	ó	Y’	=	R	*	Y
Z’		R31 R32 R33		Z		Z’				Z

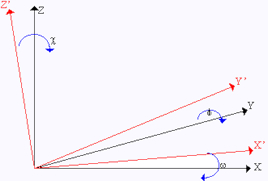
Una forma de llegar a la determinación de R es considerarla función de tres parámetros básicos: los ángulos ω, φ, y κ entendidos estos como los giros sucesivos y elementales en torno a cada uno de los ejes cartesianos (OX, OY y OZ respectivamente) que deben producirse para obtener el giro global. Esta forma de proceder permite tratar la matriz de rotación tridimensional R como una composición de tres matrices de rotación bidimensionales.

Se entenderá como giro positivo aquel que haría avanzar un sacacorchos situado sobre el eje en el sentido positivo del mismo.

---

Inicio de página½Página anterior ½Página siguiente