
INTRODUCCIÓN A LA FOTOGRAMETRÍA
ANALÍTICA
1.6. MODELOS MATEMÁTICOS
EN FOTOGRAMETRÍA ANALÍTICA
1.6.1. Helmert 2D
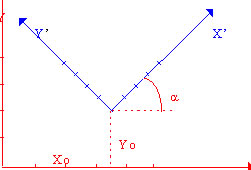
El Helmert o la Transformación de Semejanza expresa la relación que existe (o la transformación que es preciso realizar) entre dos sistemas cartesianos que discrepan en la situación del origen, en la orientación de los ejes y en la unidad de medida a lo largo de los mismos pero de manera que dicha variación en unidad de medida es constante a lo largo de cada eje y entre los dos ejes.
 |
|
 |
Igualmente puede considerarse como el modelo que da cuenta de la transformación que sufre un cuerpo al ser trasladado, girado y deformado pero de tal manera que la deformación es absolutamente homogénea (deformación radial) de manera que se conserva semejante a sí mismo
Aplicación fotogramétrica: la más frecuente es la de la Orientación Interna: paso de Coordenadas Instrumentales (como coordenadas de entrada) a Fotocoordenadas (como coordenadas de salida) siempre y cuando pueda suponerse que entre ambos sistemas hay una relación de semejanza.
El cálculo de los parámetros (fase de cálculo) puede realizarse sólo si se dispone de Fotocoordenadas de una serie de puntos. Estos puntos son las Marcas Fiduciales y la determinación de sus Fotocoordenadas es el objeto de los procesos de calibración de cámaras métricas.
Así pues, la ejecución práctica (del cálculo) de una Orientación Interna consiste en la obtención (midiendo) de las Coordenadas Instrumentales de las Marcas Fiduciales de un fotograma y en la comparación (mediante el modelo matemático correspondiente) de las mismas con las Fotocoordenadas de dichas Marcas Fiduciales tal y como quedan recogidas en los certificados de calibración que expiden las casas especializadas en esta cuestión.