INTRODUCCIÓN A LA FOTOGRAMETRÍA ANALÍTICA
1.6. MODELOS MATEMÁTICOS EN FOTOGRAMETRÍA ANALÍTICA
1.6.5. Condición de Coplanaridad
La Condición de Coplanaridad da cuenta de la relación entre
varios puntos (cinco) que se expresan en tres sistemas cartesianos.
La Condición de Coplanaridad viene a constatar la condición de colinealidad entre rayos homólogos, es decir, la condición de colinealidad que se verifica entre aquellos puntos de diferentes fotogramas pero sobre el mismo punto del objeto (dos rectas que se cortan forman un plano): Los puntos de vista de sendos fotogramas, los puntos imagen homólogos entre sí y homólogos del punto del terreno pertenecen a un mismo plano.
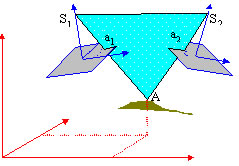
Los elementos implicados son:
- S1,
punto de vista del fotograma izquierdo, expresado tanto en el sistema
propio (Fotocoordenadas) como en el sistema del objeto
(habitualmente, Coordenadas Modelo).
- S2,
punto de vista del fotograma derecho, expresado tanto en el sistema propio
(Fotocoordenadas)
como en el sistema del objeto (habitualmente Coordenadas Modelo).
- a1,
punto imagen en el fotograma izquierdo, expresado en su propio sistema
cartesiano (Fotocoordenadas).
- a2,
punto imagen en el fotograma derecho, expresado en su propio sistema
cartesiano (Fotocoordenadas).
La condición de coplanaridad se caracteriza por no implicar,
en su formulación matemática más habitual, al punto del objeto lo que constituye
una limitación pero también la ventaja de simplificar considerablemente el
modelo matemático.
Su aplicación es el cálculo de los parámetros de la Orientación Relativa. Para ello es
preciso conocer las Fotocoordenadas (obtenidas en la fase previa de la Orientación Interna) de una serie
de puntos homólogos. La posterior fase de transformación asociada a la Orientación Relativa (obtención de
Coordenadas
Modelo) no se lleva a cabo con este modelo matemático sino mediante
la condición de colinealidad.
El sistema cartesiano asociado al objeto (Coordenadas Modelo) puede elegirse de la forma más rentable posible. Si se le hace coincidir, por ejemplo, con el sistema de Fotocoordenadas de la placa izquierda, las coordenadas objeto (modelo) del punto de vista izquierdo son ya conocidas y además la relación entre estos dos sistemas queda igualmente determinada.