Concepto

Una Proyección Cartográfica es una correspondencia biunívoca entre los puntos de la superficie terrestre y los puntos de un plano llamado Plano de proyección.

Puesto que cualquier punto de la esfera está definido por sus coordenadas geográficas (l,f) y cualquier punto del plano lo está por sus coordenadas cartesianas (X,Y), existirá una serie infinita de relaciones que liguen (l,f) con (X.Y). Cada una de estas infinitas relaciones será un sistema de proyección Cartográfico.

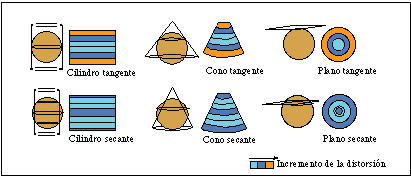
Clasificación de las Proyecciones

PURAS (Simple Proyección de la esfera o parte de ella)
POR DESARROLLO Se proyecta la esfera sobre una superficie desarrollable que puede ser tangente o secante a la esfera.	CÓNICAS	Punto de vista en el centro de la esfera. El plano de proyección es un cono tangente o secante a la esfera.
	CILINDRICAS	Punto de vista en el centro de la esfera. El plano de proyección es un cilindro tangente a la esfera a lo largo de un círculo máximo.
ACIMUTALES Toda la superficie se proyecta sobre un único plano de proyección.	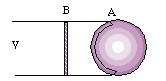ORTOGRÁFICAS	Punto de vista en el infinito.
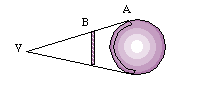	ESCENOGRÁFICAS	Punto de vista en un punto propio fuera de la esfera.
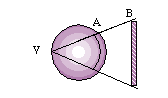	ESTEREOGRÁFICAS	Punto de vista en las antípodas del punto de tangencia del plano de proyección.
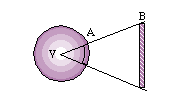	GNOMÓNICAS	Punto de vista en el centro de la esfera.
POLIEDRICAS División de la superficie terrestre en trapecios esféricos. Plano de proyección tangente al punto medio del trapecio. Punto de vista o centro de proyección en el infinito.
MODIFICADAS
CILINDRICAS	Cilindrica modificada de Mercator Universal Transversa Mercator (U.T.M.) Cilindrica equivalente
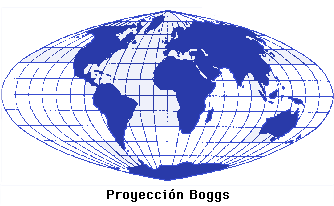
CÓNICAS	Proyección de Bonne Conforme de Lambert Equivalente de Mollweide
ACIMUTALES	Equidistante de Postell Equivalente de Lambert Policónicas

Mantenimiento de las propiedades

En el paso de la esfera al plano resultará imposible mantener todas las propiedades geométricas: ángulos, superficies y distancias se verán distorsionadas.

Conformidad	Si un mapa mantiene los ángulos que dos líneas forman en la superficie terrestre, se dice que la proyección es conforme. El requerimiento para que haya conformidad es que en el mapa los meridianos y los paralelos se corten en ángulo recto y que la escala sea la misma en todas las direcciones alrededor de un punto, sea el punto que sea. El término "mapa conforme" es a veces erróneo pues las condiciones de conformidad pueden llevarse a cabo sólo en pequeñas áreas de un mapa plano. La forma de grandes continentes mostradas en el plano difieren de la forma que tienen en el globo.
Equivalencia	Equivalencia es la condición por la cual una superficie en el plano de proyección tiene la misma superficie que en la esfera. La equivalencia no es posible sin deformar considerablemente los ángulos originales. Por lo tanto, ninguna proyección puede ser equivalente y conforme a la vez.
Equidistancia	Cuando una proyección mantiene las distancias entre dos puntos situados sobre la superficie del Globo (representada por el arco de Círculo Máximo que las une) se denomina equidistante. Es posible diseñar mapas que tengan esta característica, pero las distancias correctas sólo podrán ser medidas desde un punto, o dos como máximo. Las distancias entre otros puntos no serán correctas.

Ver Comparación Gráfica de Proyecciones más conocidas con sus respectivas deformaciones.

Las Proyecciones Cilíndricas

Las proyecciones cilíndricas se basan en el artificio de circunscribir un cilindro alrededor de la esfera terrestre. Este cilindro es tangente a la esfera a lo largo de un círculo máximo.

Cuando desarrollamos el cilindro cortándolo a lo largo de una de sus generatrices, se transforma en un rectángulo, uno de cuyos lados es la longitud del círculo máximo terrestre (2pR).

En todas las proyecciones de este grupo, los paralelos son líneas rectas, cuya longitud es la misma que la del Ecuador, mientras que los meridianos son también líneas rectas paralelas separados entre sí una longitud que es correcta sólamente en el Ecuador. Paralelos y meridianos se cortan entre sí ortogonalmente.

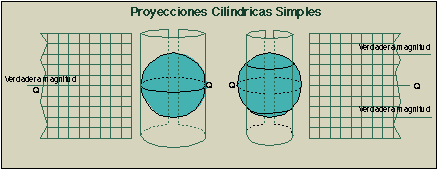
En la Proyección Cilíndrica Simple (centro de proyección en el centro de la Tierra), y el cilindro tangente al Ecuador. La separación entre paralelos y el Ecuador, vendrá definida sólamente por la latitud del paralelo. También podríamos arrollar este cilindro, de forma que fuera secante a dos paralelos.

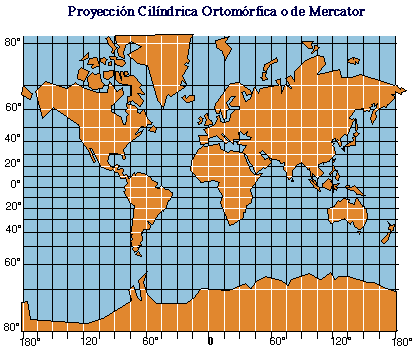
En la Proyección Cilíndrica Ortomórfica, la separación entre paralelos se hace aumentar progresivamente hacia los Polos. El espaciamiento en este caso se hace de forma que en cualquier punto de la proyección, la escala a lo largo del meridiano sea la misma que la escala a lo largo del paralelo.

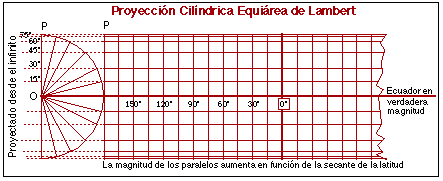
En la Proyección Cilíndrica Equiárea, la separación entre paralelos irá disminuyendo conforme nos acerquemos a los Polos: La reducción de la escala a lo largo del meridiano es compensada exactamente por el aumento de la escala a lo largo del paralelo.

Las Proyecciones Cónicas

Las proyecciones cónicas se producen al arrollar un cono sobre la superficie de la Tierra y proyectar los puntos sobre él. El eje del cono coincide con el eje de los polos, y el contacto de cono y esfera se produce a lo largo de un paralelo llamado estándar (también puede ser secante obteniendo dos paralelos estándar).

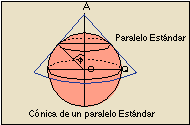
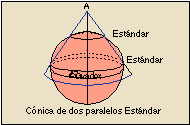
En las proyecciones cónicas (siempre que el eje del cono coincida con el eje de los polos) los meridianos aparecen como rectas concurrentes y los paralelos como circunferencias concéntricas. Entre las Proyecciones Cónicas más importantes citaremos la Proyección Bonne, la Cónica Conforme de Lambert y la Proyección Cónica Equivalente de Lambert.

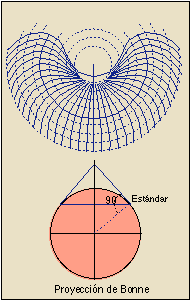
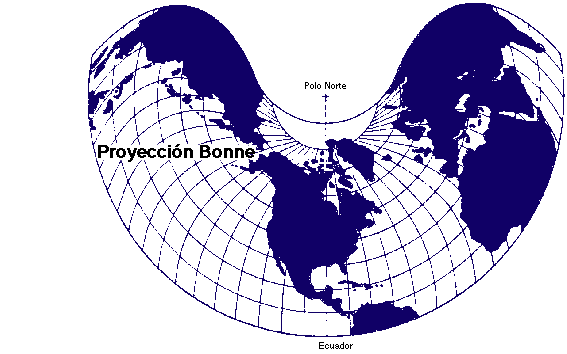
La Proyección de Bonne es un caso particular de la de un paralelo estándar consiguiéndose una Proyección equiárea. No es exactamente una proyección cónica -puesto que los meridianos no se representan como rectas concurrentes sino como arcos- pero se aproxima bastante al ser los paralelos círculos concéntricos.

Análisis de las Deformaciones

El mapa deberá ser equivalente o conforme y ya sabemos que ambas propiedades son excluyentes. La elección que se haga dependerá del uso que se vaya a dar al mapa.

Las proyecciones conformes muestran normalmente una distorsión de las superficies en tanto que las equivalentes muestran deformaciones angulares.

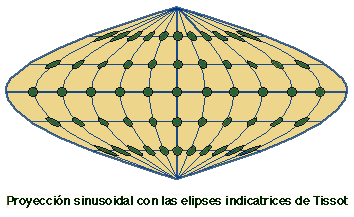
Para evaluar las deformaciones se utiliza el denominado Artificio de Tissot, consistente en constatar las deformaciones sufridas por un círculo elemental de terreno. El resultado son las conocidas elipses de error en las que la magnitud y dirección de sus ejes nos indican las direcciones de máxima y mínima deformación.

Enlaces

Map Projection Overview The Geographer´s Craft project. Universidad de Texas.Texto e Imágenes. Map Projection Home Page Dr. Keith C.Clarke. Hunter College, City University of New York Texto e Imágenes. Enlaces. Software. Bibliografía. Georeferencing Principles Fórmulas e Imágenes. Geography 3530 Universidad de Nebraska. Texto e Imágenes. Exámenes. Map Projections Hans Zuuring. Texto y ejemplos. Preguntas. Map Projections, Co-Ordinate Systems and GPS Centre for Earth Observation (CEO) . Texto e Imágenes. Fundamentals of cartography National Atlas Information Service de Canada. Texto e Imágenes. Glosario. The Properties and Uses of Selected Map Projections US.Geological Survey. Texto e Imágenes. 3G on W3: The Great Globe Gallery Imágenes a color de las proyecciones de mapas más importantes.